Introduction
In machine studying and synthetic intelligence, adversarial assaults have gained a lot consideration from researchers. These assaults alter the inputs to mislead the mannequin into making flawed predictions. Amongst these, the Quick Gradient Signal Methodology (FGSM), is especially price mentioning due to its effectiveness and ease .
The importance of FGSM lies in its potential to reveal the vulnerability of contemporary fashions to minor variations in enter knowledge. These perturbations, which steadily go unnoticed by human observers, inflict errors on prediction accuracy. Understanding and minimizing these vulnerabilities is pivotal to constructing fault-resistant machine studying programs trusted in sensible functions like autonomous driving, healthcare provisioning, and safety administration.
This compelling article takes a deep dive into the which means of FGSM and elucidates its mathematical foundations with readability and precision. It supplies demonstrations by an illustrative case research.
First-Order Taylor Growth in Adversarial Assaults
The utilization of the First-Order Taylor Growth approach in approximating the loss perform is a major methodology to know how slight modifications in enter can have an effect on the loss in machine studying fashions. This strategy, significantly helpful when coping with adversarial assaults, includes computing an approximation of L(x+δ) utilizing its gradient with Taylor enlargement round x:
L(x+δ) ≈ L(x) + ∇L(x) ⋅ δ
- The loss on the unique enter x is denoted as L(x), the gradient of the loss perform at x is represented by ∇L(x), and δ is a small perturbation to x.
- The route and price of the steepest improve of the loss perform is represented by ∇L(x). By perturbing x within the route of ∇L(x), we are able to predict how the loss perform will change.
Adversarial assaults use the Taylor Growth to seek out perturbations δ that maximize the loss perform L(x+δ). That is achieved by selecting δ proportional to the signal of ∇L(x):
δ = ϵ ⋅ signal(∇L(x))
the place ϵ is a small scalar controlling the magnitude of the perturbation.
For illustration objective, let’s draw a diagram to characterize the First-Order Taylor Growth of the loss perform. It will embody the loss curve, the unique level, the gradient vector, the perturbed level, and the first-order approximation.
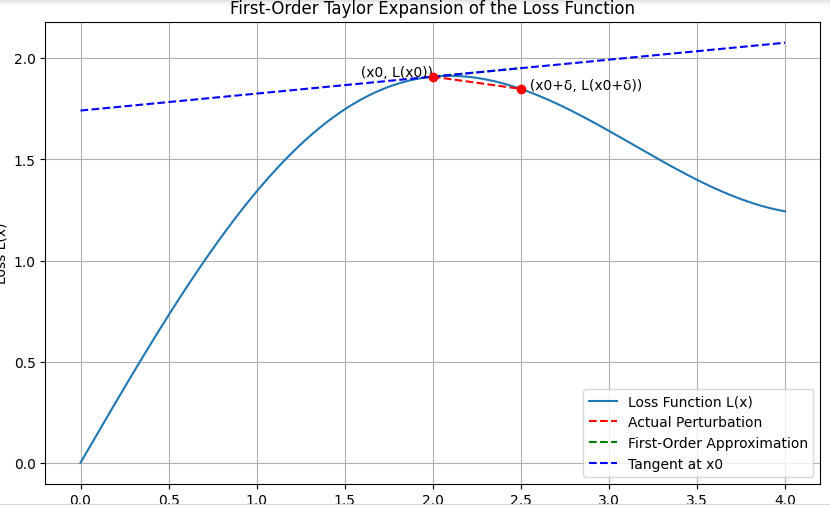
The diagram generated illustrates the important thing ideas of the First-Order Taylor Growth of the loss perform. Listed below are the principle takeaways:
- Loss Curve (L(x)): A easy curve representing the loss perform over totally different inputs.
- Unique Level (x0, L(x0)): The purpose on the loss curve which corresponds to the worth of the enter x0.
- Gradient Vector (∇L(x0)): This represents the slope of the tangent line on the level L(x0).
- Perturbed Level (x0 + δ, L(x0 + δ)): The brand new level after including a small perturbation δ to the enter x0.
- First-Order Approximation (L(x0) + ∇L(x0) ⋅ δ): The linear approximation of the loss perform round x0.
We are able to see how the gradient of the loss perform can be utilized to approximate the change in loss as a consequence of small perturbations within the enter. This understanding is essential for producing adversarial examples within the context of adversarial assaults.
The Quick Gradient Signal Methodology (FGSM) is predicated on the precept of utilizing the gradients of the loss perform with respect to the enter knowledge to find out the route wherein the enter must be modified to extend the mannequin’s error. The steps concerned in FGSM could be described within the picture beneath:
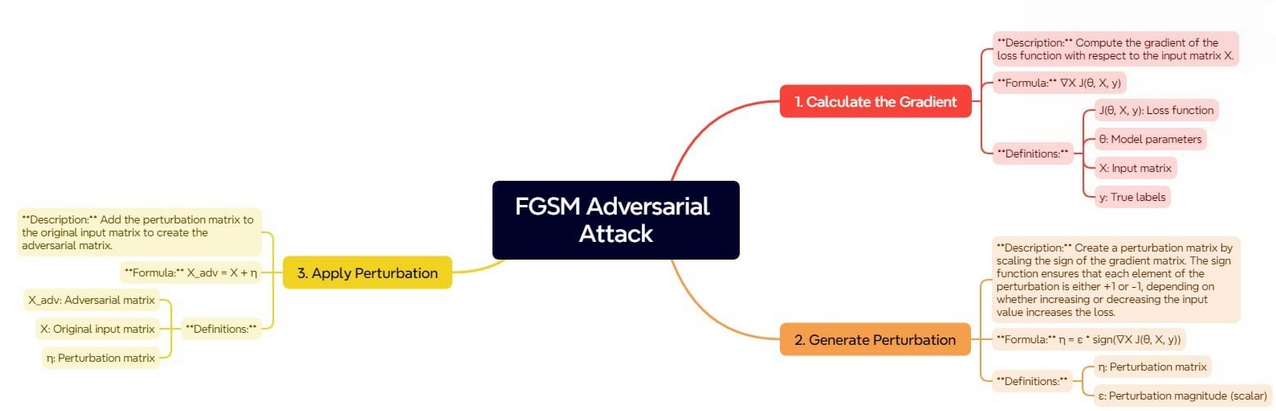
This course of begins by figuring out the gradient of the loss perform with respect to the enter knowledge. The gradient defines how the loss perform would change if the enter knowledge have been barely modified. Understanding this relationship, we are able to outline the route wherein small shifts in inputs will improve the loss.
As soon as the gradient is computed, the subsequent step is to generate the perturbation. That is achieved by scaling the signal of the gradient. The signal perform ensures that every part of the perturbation matrix is both + or – 1. This means whether or not the loss is most delicate to a rise or a lower of the corresponding enter worth.
The scaling issue ensures that these perturbations must be small however giant sufficient to idiot the mannequin.
The final step is to generate the adversarial instance by making use of this perturbation to the unique enter. By including the perturbation matrix to the unique enter matrix, we get the enter that appears similar to the unique knowledge however is constructed to mislead the mannequin into making incorrect predictions.
Makes use of and Significance of FGSM in Machine Studying
Let’s take into account some objective for which we are able to use Quick Grdient Sigh Methodology:
- Testing Mannequin Robustness: FGSM is uded to evaluate machine studying mannequin resilience by testing it in opposition to adversarial assaults. This helps establish and repair potential vulnerabilities to enter knowledge modifications.
- Enhancing Mannequin Safety:Strong fashions are key in safety apps like self-driving, healthcare, and finance. FGSM assessments mannequin power by exposing vulnerability to assaults. Very important for safety-critical functions with reliance on dependable fashions.
- Adversarial Coaching: It helps in adversarial coaching, bettering mannequin robustness by exposing it to potential assaults throughout coaching. This enhances its efficiency on perturbed inputs.
- Understanding Mannequin Conduct: FGSM helps perceive mannequin conduct throughout enter perturbations, resulting in improved design and coaching for dependable programs.
- Benchmarking Adversarial Protection Methods: It’s utilized by researchers to check protection strategies in opposition to adversarial assaults for growing strong safety.
- Benchmarking Adversarial Protection Methods: It exposes vulnerabilities in programs like picture recognition and pure language processing, driving growth of safer ML functions throughout industries.
- Instructional Functions: It is usually used for schooling, serving as a fundamental introduction to adversarial assaults and defenses in machine studying. Understanding FGSM supplies people with foundational information of extra superior strategies, permitting them to contribute to the sector.
Sensible Implementation
To exemplify the Quick Gradient Signal Methodology (FGSM) assault virtually, we are going to use TensorFlow to generate adversarial examples. We are going to use Gradio as an interactive show device to showcase the outcomes. We’ll use a picture of a yellow Labrador retriever, which could be discovered right here.
First, let’s load the required libraries and the picture:
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
import gradio as gr
import requests
from PIL import Picture
from io import BytesIO # Load the picture
image_url = "https://storage.googleapis.com/obtain.tensorflow.org/example_images/YellowLabradorLooking_new.jpg"
response = requests.get(image_url)
img = Picture.open(BytesIO(response.content material))
img = img.resize((224, 224))
img = np.array(img) / 255.0 # Show the picture
plt.imshow(img)
plt.present() Output:
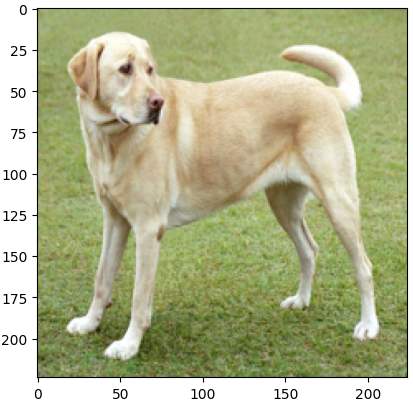
The above Python code helps to load and look at a picture from a particular URL by utilizing frameworks corresponding to TensorFlow, NumPy, Matplotlib, and PIL. It makes use of the requests library to fetch the picture, resizes it to a 224*224, and normalizes the worth of pixels between Zero and 1, earlier than changing the picture right into a numpy array.
Lastly, customers can show the picture and make sure the program appropriately hundreds and processes the picture.
Subsequent, let’s load a pre-trained mannequin and outline the FGSM assault perform:
# Load a pre-trained mannequin
mannequin = tf.keras.functions.MobileNetV2(weights='imagenet') # Outline the FGSM assault perform
def fgsm_attack(picture, epsilon): picture = tf.convert_to_tensor(picture, dtype=tf.float32) picture = tf.expand_dims(picture, axis=0) with tf.GradientTape() as tape: tape.watch(picture) prediction = mannequin(picture) loss = tf.keras.losses.categorical_crossentropy(tf.keras.utils.to_categorical([208], 1000), prediction) gradient = tape.gradient(loss, picture) signed_grad = tf.signal(gradient) adversarial_image = picture + epsilon * signed_grad adversarial_image = tf.clip_by_value(adversarial_image, 0, 1) return adversarial_image.numpy().squeeze() # Show the adversarial picture
adversarial_img = fgsm_attack(img, epsilon=0.08)
plt.imshow(adversarial_img)
plt.present()ouput:
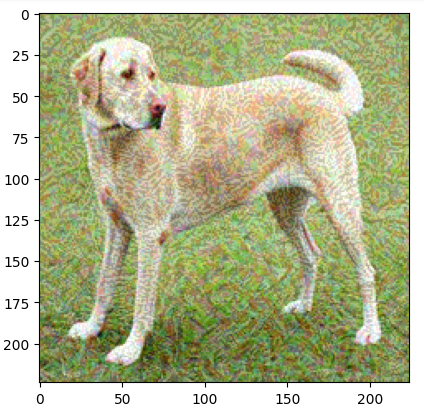
The code above demonstrates how you can use the FGSM adversarial assault on a picture. It begins by downloading a pre-train mobileNetV2 mannequin with Imagenet weights.
The fgsm_attack methodology is then outlined to carry out the adversarial assault. It transforms the enter picture right into a tensor, performs the computational work to find out the mannequin’s prediction, and computes the loss with respect to the goal label.
By utilizing TensorFlow’s gradient tape, the loss with respect to the picture enter is computed, and its signal is used to create perturbation. That is added to the unique picture with a multiplicative issue of epsilon to get an adversarial picture. The adversarial picture is then clipped to stay within the legitimate pixel vary.
Lastly, let’s combine this with Gradio to permit interactive exploration of the adversarial assault:
# Outline the Gradio interface
def generate_adversarial_image(epsilon): adversarial_img = fgsm_attack(img, epsilon) return adversarial_img interface = gr.Interface( fn=generate_adversarial_image, inputs=gr.Slider(minimal=0.0, most=0.1, worth=0.01, label="Epsilon"), outputs=gr.Picture(kind="numpy", label="Adversarial Picture"), reside=True
) # Launch the Gradio interface
interface.launch()Output
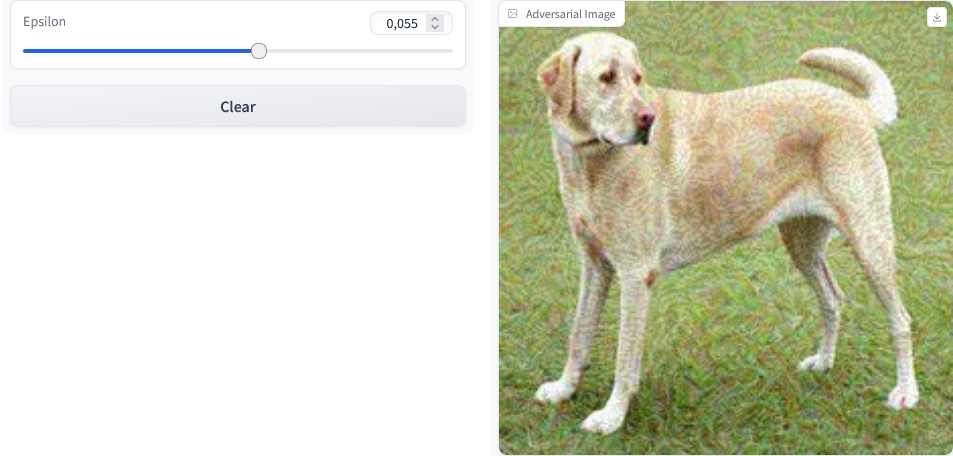
The code above generates a generate_adversarial_image perform. It accepts the epsilon worth as its parameter and executes the FGSM assault on the picture, then outputs the adversarial picture.
Our Gradio interface is custom-made with a slider enter that enables for modification of the epsilon worth whereas additionally displaying updates in real-time through reside=True parameter setting.
The command interface.launch() begins the web-based Gradio platform the place customers can manipulate numerous levels of values. This allows them to see corresponding opposed photographs generated by their inputs till they discover what fits them finest.
Comparability Between FGSM and Different Adversarial Assault Strategies
The desk beneath summarizes the comparability between FGSM and different adversarial assault strategies:
| Assault Methodology | Description | Execs | Cons |
|---|---|---|---|
| FGSM | Easy, environment friendly, makes use of gradient signal to generate adversarial examples | Fast, simple to implement, good for preliminary vulnerability evaluation | Produces simply detectable perturbations, much less efficient in opposition to strong fashions |
| PGD | Iterative model of FGSM, refines perturbations over a number of steps | Simpler at discovering adversarial examples, more durable to defend in opposition to | Computationally costly, time-consuming |
| CW | Carlini & Wagner assault, minimizes perturbations to be much less detectable | Very efficient, produces minimal perturbations | Complicated to implement, computationally intensive |
| DeepFool | Finds minimal perturbations to maneuver enter throughout choice boundary | Produces small perturbations, efficient for a lot of fashions | Extra computationally costly than FGSM, much less intuitive |
| JSMA | Jacobian-based Saliency Map Assault, targets particular pixels for perturbation | Efficient at creating focused assaults, can management which pixels are modified | Complicated, could be sluggish, requires detailed understanding of mannequin |
FGSM is most well-liked for quick computation and ease in finishing up preliminary robustness assessments and adversarial studying. In distinction, to create highly effective adversarial examples, strategies corresponding to PGD, or C&W can be utilized though they’re computationally costly. Strategies like DeepFool and JSMA are extra appropriate for observing minimal perturbations and have significance however devour extra computational energy.
Conclusion
This text explores the Quick Gradient Signal Methodology (FGSM), an important approach in adversarial machine studying. This methodology exposes neural networks’ vulnerabilities to minor enter alterations by computing gradients with respect to the loss perform. The ensuing perturbations can drastically affect mannequin predictions. This makes understanding FGSM’s mathematical basis essential to creating resilient machine studying programs that do not buckle beneath assault. It is essential to imbue our essential functions with a sturdy protection mechanism in opposition to such assaults.
The sensible implementation utilizing TensorFlow and Gradio illustrates FGSM’s real-world utility. Customers can simply tinker with various epsilon values to witness how these changes form adversarial picture output. Such an instance serves as a stark reminder of FGSM’s effectivity whereas equally underlining AI system vulnerability to malicious assaults. There’s a want for strong safety measures that assure optimum security and reliability in programs’ operations.
References
Adversarial instance utilizing FGSM
Adversarial Assaults and Defences: A Survey